El hombre que pesó la Tierra

Cuando Maxwell se puso a estudiar los manuscritos de Henry Cavendish quedó maravillado. Cavendish había sido un científico reconocido en su época (100 años antes de Maxwell), pero Maxwell se encontró con el trabajo de un genio. 

Henry Cavendish era extremadamente tímido y reservado, hablaba con un tono agudo y apurado, se comunicaba con la gente a su servicio mediante notas, se vestía siempre con un blazer violeta y un sombrero de tres picos que eran la moda de 50 años antes. Y cuando se le gastaban, encargaba unos idénticos. Sólo se transformaba cuando hablaba de ciencia, en las reuniones de la Royal Society, donde todos sus colegas valoraban su conocimiento y profundidad. Era inmensamente rico, y cuando murió su cuenta era la más abultada del Banco de Inglaterra. Salvo por esto último, ¡estoy seguro de que todos mis colegas conocen a alguien así!

En 1798 publicó los resultados de su experimento más recordado. Lo que reportó fue la densidad de la Tierra, que era una magnitud importante para las detalladas tareas de geodesia que empezaban a cubrir el planeta en esos años, pero él lo llamaba pesar el mundo. Su resultado, 5.448 veces la densidad del agua, con precisión de un 0.5%, no fue mejorado hasta más de 100 años después. Para hacerlo usó un aparato que había heredado del naturalista Rev. John Michell (el primero que imaginó los agujeros negros). 

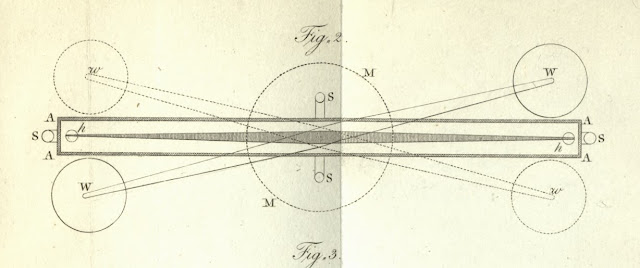
La idea es medir la atracción gravitatoria entre las bolas grandes y las chicas que se ven en el dibujo. Las grandes están fijas (están colgadas, pero fijas) y las chicas están montadas en un brazo horizontal que cuelga de un cable. El aparato se llama balanza de torsión. La fuerza de atracción afecta la manera en que las bolas chicas oscilan para un lado y para el otro, torsionando el cable de suspensión. Cada oscilación duraba más de 10 minutos, y Cavendish las observaba durante más de 2 horas a través de un telescopio desde fuera del laboratorio, que se mantenía completamente oscuro y aislado para no afectar el sutil movimiento con corrientes de aire o fuentes de calor.

El paper de Cavendish tiene 60 páginas, y está escrito de una manera arcaica y difícil de seguir hoy en día. Newton y Cavendish entendían la gravedad de la misma manera que nosotros (bueno, la gravedad newtoniana, no la Relatividad General, obvio), pero no escribían las ecuaciones de la manera que lo hacemos ahora. Una versión modernizada de lo que hizo sería la siguiente. Newton había descubierto la ley de gravitación universal: que entre dos objetos cualesquiera existe una fuerza de atracción, proporcional a sus masas, e inversamente proporcional al cuadrado de su separación. En fórmula:

\[ F = G \frac{m_1 m_2}{r^2}, \]

donde \(F\) es la fuerza, \(m_1\) y \(m_2\) son las masas y \(r\) es la distancia entre ellas. La constante \(G\) es la constante de la proporcionalidad del enunciado. Conociendo las masas de las bolas y su separación, el movimiento medido por Cavendish permite deducir la fuerza de atracción, y por lo tanto la constante \(G\), que resulta ser pequeñísima en unidades convencionales:

\[ G = 0.000000000067~\mathrm{N m}^2/\mathrm{kg}^2.\]

En otras palabras, dos bolas de 1 kg cada una, puestas a un metro una de la otra, se atraen con una fuerza de 0.000000000067 N (newtons, unos 100 gramos). Ahora bien, la ley de Newton es universal, así que la misma constante se aplica a la atracción entre la Tierra y cualquier objeto que ella atrae: una manzana de masa \(m\), por ejemplo, en la superficie de la Tierra. Esa fuerza es el peso de la manzana, que es su masa por la aceleración de la gravedad (\(g\), los 9.8 m/s\(^2\), conocidos desde la época de Galileo). Así que tenemos:

\[ m\,g = G \frac{m M}{R^2},\]

de donde se puede despejar \(M\), la masa de la Tierra. La relación entre la masa y la densidad es trivial, si uno conoce el tamaño de la Tierra, su radio \(R\). Jean Picard (no Jean Luc Picard, eh) había medido con enorme precisión la longitud de un grado del meridiano de París en 1742, así que \(R\) era un valor bien conocido en la época de Cavendish. La masa de la Tierra resulta enorme:

\[M = 6\,000\,000\,000\,000\,000\,000\,000\,000~\mathrm{toneladas}.\]

Este enorme número, junto con la pequeñez de la constante \(G\), ponen de manifiesto un hecho tan trivial como sorprendente: la fuerza de la gravedad, que es la más familiar de las fuerzas de la naturaleza, ¡es pequeñísima! Hagan el siguiente experimento. Tomen un clip o un alfiler, y suéltenlo en el aire. ¿Qué pasa? Cae. Cae porque la Tierra lo atrae. Ahora tomen un imancito, por ejemplo de la puerta de la heladera, y peguen el clip o alfiler al imán. ¿Qué pasa? No se cae. Ese imancito, que pesa un par de gramos, hace una fuerza (magnética) capaz de contrarrestar la fuerza gravitatoria que ejerce la Tierra entera, con sus trillones de toneladas. Esta discrepancia entre las fuerzas de gravedad y electromagnéticas es un misterio, para el cual no tenemos una explicación.

Cavendish hizo contribuciones valiosas en distintas áreas de la ciencia. En 1766, fue el primero en aislar el hidrógeno y en reconocer que el agua era un compuesto de hidrógeno y oxígeno. Poco después demostró que el aire era mayormente nitrógeno y oxígeno, con otros gases en cantidades mucho menores. Sus trabajos abarcan la astronomía, la meteorología, la termodinámica y la naturaleza de la electricidad. Maxwell descubrió, en sus manuscritos, que además de sus muchas contribuciones conocidas, Cavendish había realizado una cantidad de descubrimientos que quedaron en secreto, y que se atribuyen a otros pioneros, tales como la ley de Ohm de la resistencia eléctrica, la ley de Dalton de presiones parciales, la ley de Coulomb de las fuerzas eléctricas, y la ley de Charles de los gases. Así que decidió cambiar el nombre del Laboratorio de Física que estaba organizando para la Universidad de Cambridge, y llamarlo Laboratorio Cavendish, del cual ya hemos contado la historia en El viejo Cavendish y La edad de oro del Cavendish.

 

---

El retrato de Cavendish es de la portada de una biografía suya del siglo XIX.

Los diagramas de la balanza de torsión de Cavendish son de su paper, Experiments to determine the density of the earth, Phil. Trans. 88:469 (1798).